在承受机械载荷时,材料的刚度与疲劳门槛值都是重要的属性。对于单网络的弹性体和单网络的水凝胶来说,随着网络链长增加,材料的刚度降低而疲劳门槛值增加,因此不可能同时实现高刚度和高疲劳门槛值。哈佛大学锁志刚教授与西安交大软机器实验室提出,通过引入双网络体系解决刚度-疲劳门槛值这一矛盾,并通过双网络水凝胶加以证实。在双网络水凝胶中,刚度依赖于短链网络,而疲劳门槛值依赖于长链网络。一旦刚度与疲劳门槛值由不同网络控制,刚度-疲劳门槛值的矛盾就不复存在。已有实验数据表明,双网络水凝胶的刚度与短链网络的链长成反比。该研究通过制备五种不同长链网络链长的双网络水凝胶并测量疲劳门槛值,发现疲劳门槛值与长链网络链长的1/2次方成正比。这些实验结果表明双网络体系的引入可以有效解决刚度-疲劳门槛值的矛盾,使得弹性体与水凝胶同时实现高刚度与高门槛值。
1 弹性体网络中的刚度-疲劳门槛值矛盾
刚度-疲劳门槛值的矛盾对于单网络材料来说是固有的。单网络弹性体的杨氏模量可由E=3kT/(Vnι) 来估计,其中k为玻尔兹曼常数,T 为温度,V 为单体体积,n 为链长,即每个聚合物链上单体数目,ι 为单体长度。单网络弹性体的疲劳门槛值由经典的Lake-Thomas模型预计,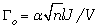 ,其中 α 为无量纲系数,J 为分子链中单个共价键的键能。随着链长增加,弹性体的刚度随链长减小,E~1/n,而疲劳门槛值随链长增加,
,其中 α 为无量纲系数,J 为分子链中单个共价键的键能。随着链长增加,弹性体的刚度随链长减小,E~1/n,而疲劳门槛值随链长增加,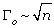 ,因此刚度与疲劳门槛值有
,因此刚度与疲劳门槛值有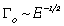 的关系,单网络弹性体无法同时存在高模量与高的疲劳门槛值。单网络水凝胶由水分子与柔性聚合物网络组成,其杨氏模量可以由
的关系,单网络弹性体无法同时存在高模量与高的疲劳门槛值。单网络水凝胶由水分子与柔性聚合物网络组成,其杨氏模量可以由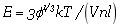 估计,疲劳门槛值可由
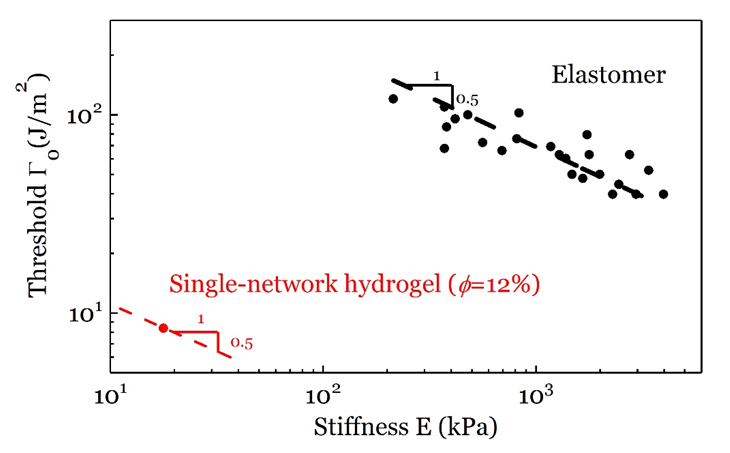
估计,疲劳门槛值可由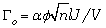 预计,其中Φ 为聚合物的体积分数,因此刚度-疲劳门槛值矛盾仍然存在。文献中测得的单网络弹性体的刚度与疲劳门槛值数据证实了这一矛盾的存在。
预计,其中Φ 为聚合物的体积分数,因此刚度-疲劳门槛值矛盾仍然存在。文献中测得的单网络弹性体的刚度与疲劳门槛值数据证实了这一矛盾的存在。
2 刚度-疲劳门槛值矛盾的一种解决方法
单网络材料中刚度-疲劳门槛值矛盾的存在是由于这两个材料属性都由同一变量——高分子网络的链长来控制。假定双网络材料中短链网络链长为 nA,长链网络链长为 nB。一旦刚度与疲劳门槛值由不同网络控制,刚度依赖于短链网络链长,E~1/nA,疲劳门槛值依赖于长链网络链长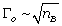 ,刚度-疲劳门槛值的矛盾就不复存在。
,刚度-疲劳门槛值的矛盾就不复存在。
该研究采用日本北海道大学龚剑萍教授课题组提出的经典双网络水凝胶来证实这一假设。该水凝胶由长链、柔性的聚丙烯酰胺PAAm网络与短链、刚性的聚-2丙烯酰胺-2甲基丙磺酸PAMPS网络组成。两个网络拓扑缠绕在一起。当水凝胶被拉伸,短链网络承受绝大多数载荷并且提供刚度,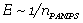 。当承受循环载荷时,裂纹尖端的应力集中使得裂纹尖端的PAMPS网络在早期的循环中就断裂成簇,疲劳裂纹扩展只依赖于PAAm长链网络,因此PAAm-PAMPS的疲劳门槛值依赖于长链的PAAm网络的链长
。当承受循环载荷时,裂纹尖端的应力集中使得裂纹尖端的PAMPS网络在早期的循环中就断裂成簇,疲劳裂纹扩展只依赖于PAAm长链网络,因此PAAm-PAMPS的疲劳门槛值依赖于长链的PAAm网络的链长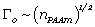 。
。

3双网络水凝胶刚度/疲劳门槛值实验结果
双网络水凝胶的刚度与短链PAMPS网络的链长的关系已经被龚剑萍课题组研究,研究结果证实双网络水凝胶刚度与PAMPS网络链长成反比。
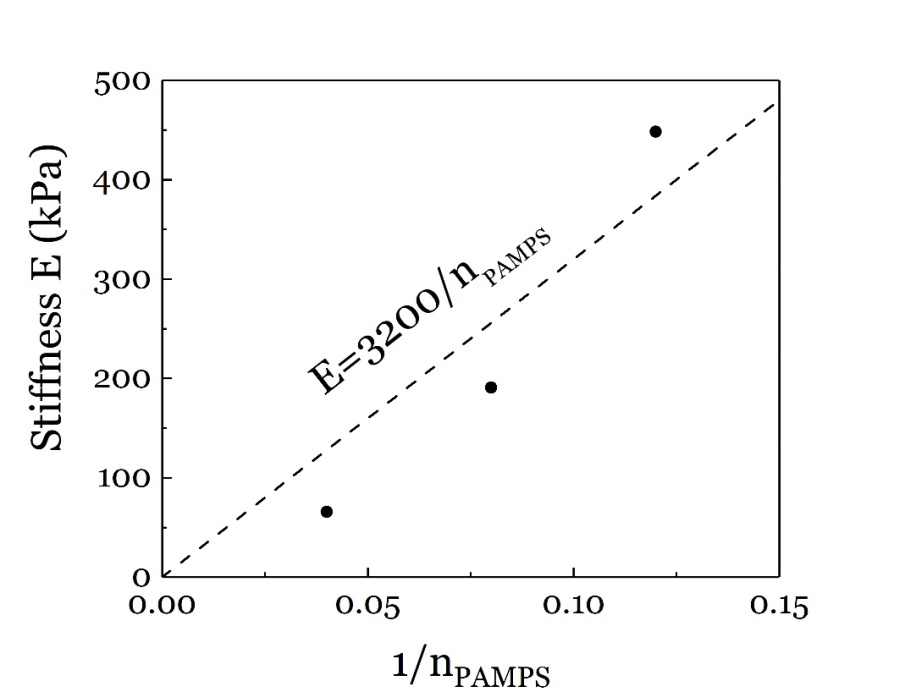
为探究疲劳门槛值的影响因素,该研究通过改变交联剂亚甲基双丙烯酰胺MBAA浓度与丙烯酰胺单体AAm浓度的比例,制备了五种不同PAAm链长的双网络水凝胶,链长n分别为500,5000,13889,27778,50000。采用纯剪切测试方法,不带裂纹试样在循环载荷下的应力应变曲线有明显滞回,发生疲劳损伤,这是由短链PAMPS网络的断裂造成的;带裂纹试样在循环载荷下发生疲劳裂纹扩展直至断裂。对于给定PAAm链长的试样,测试计算在不同最大循环拉伸比下的能量释放率G与裂纹扩展速率dc/dN关系,进而获得疲劳门槛值。将疲劳门槛值作为纵轴,PAAm网络链长的1/2次方作为横轴,发现水凝胶的疲劳门槛值与链长的1/2次方成正比。这一结果与Lake-Thomas模型的理论预测吻合。

4结论
单网络弹性体和单网络水凝胶存在刚度-疲劳门槛值矛盾,这一矛盾在双网络材料中可以得到解决。通过制备五种不同长度的PAAm网络的PAAm-PAMPS双网络水凝胶,测量不带裂纹试样在循环载荷作用下的疲劳损伤和带裂纹试样的疲劳断裂,证明了PAAm-PAMPS双网络水凝胶的疲劳门槛值正比于PAAm网络的链长的1/2次方,符合Lake-Thomas模型预测。而该水凝胶的的刚度由PAMPS短链网络决定。因此,通过独立控制两个网络的链长可以解决刚度-疲劳门槛值矛盾。
在设计特定的应用结构时,需要不同的材料性能组合,如刚度、强度、断裂应变、断裂韧性和疲劳门槛值。双网络水凝胶高的断裂韧性一直以来受到人们的重视。该研究探索得出双网络水凝胶具有另一个重要特性:可有效解决刚度-门槛值矛盾,这可以作为设计高刚度和高疲劳门槛值水凝胶和弹性体的一般原则。

这一研究工作最近发表在ASME Journal of Applied Mechanics纪念断裂力学100周年专刊。论文的第一作者为西安交通大学硕士研究生周一帆,共同作者包括西安交大博士研究生张雯蕾、胡建教授、唐敬达博士、本科生金宸宇。西安交通大学卢同庆教授和美国科学院院士、美国工程院院士、哈佛大学锁志刚教授为共同通讯作者。
论文链接:
Zhou et al. The Stiffness-threshold Conflict in Polymer Networks and a Resolution. ASME Journal of Applied Mechanics 2019.
https://doi.org/10.1115/1.4044897
1 Treloar, R., The Physics of Rubber Elasicity. 1974.
2 Lake, G.J.andThomas, A.G.,1967, "The Strength of Highly Elastic Materials", Proc. R. Soc. London, Ser., A, 108-119.
3 Ahmed, S.,Nakajima, T.,Kurokawa, T.,Anamul Haque, M.andGong, J.P.,2014, "Brittle–Ductile Transition of Double Network Hydrogels: Mechanical Balance of Two Networks as the Key Factor", Polymer, 55, 914-923.
4 A.K.Bhowmick,1988, "Threshold Fracture of Elastomers", Journal of macromolecular Science,Part C:Polymer Reviews, 28, 339-370.
5 Zhang, E.,Bai, R.,Morelle, X.P.andSuo, Z.,2018, "Fatigue Fracture of Nearly Elastic Hydrogels", Soft Matter, 14, 3563-3571..
6 Zhang, W.L.,Hu, J.,Tang, J.D.,Wang, Z.T.,Wang, J.K.,Lu, T.Q.andSuo, Z.G.,2018, "Fracture Toughness and Fatigue Threshold of Tough Hydrogels", ACS Macro Letters, 17-23.
- 北京化工大学胡君教授团队 Small:兼具高拉伸与稳固界面性的一体化拉胀导电弹性体复合材料 2025-05-18
- 清华徐军课题组 Small: 通过多级氢键设计制备高强韧、抗冲击多功能弹性体 2025-05-13
- 华南师大张振 JCIS:以聚多巴胺包覆纤维素纳米晶和MXene为光热纳米增强填料的液晶弹性体基光致软致动器 2025-05-12
- 北理工陈煜/积水潭医院李波 CEJ: 仿蜗牛粘液强粘附水凝胶髓内钉止血涂层 2025-02-05
- 长安大学颜录科、西工程大张鹏飞 JMCA:自修复、抗变形MXene双网络水凝胶用于稳定太阳能驱动界面蒸发 2025-01-27
- 湖工大李学锋/北理工夏敏 Nano Lett.:坚固、抗污的亲水微凝胶增强双网络水凝胶 - PVDF互穿微滤膜 2024-12-16
- 天津科技大学程博闻教授团队 Macromolecules:锚定二酐结构-PBO膜反trade-off现象 2025-03-06
